Вопрос по математике:
1. При параллельном переносе на вектор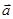 
четырехугольник АВСD перешел в четырехугольник А1В1С1D1. Найти координаты точек А1, В1, С1, если А(4; 5), В(7; 0); С(– 1; – 4), D(– 4; 7), D1(– 2; 5).
2.Составить уравнение образа окружности х2 + у2 – 4х + 6у – 13 = 0 на вектор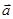 
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок - бесплатно!
- 12.03.2024 09:30
- Математика
- remove_red_eye 1475
- thumb_up 3
Ответы и объяснения 0
Знаете ответ? Поделитесь им!
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.