2 способа, зависит от того, прошли ли вы уже вписанную/описанную окружность. Если нет - то пиши второй способ. 

1 способ: Надо доказать, что BO = AO = OC

Рассмотрим прямоугольный треугольник ABC (угол B - прямой, BO - медиана). Угол B опирается на дугу AB, а так как угол B - вписанный, то дуга AB равна 2*уголB = 180. Следовательно AC - диаметр, а центр AC - центр окружности. Но окружность так же проходит по точке B. А значит AO = OC = OB = r - радиус описанной окружности. 

Доказано. 

2 способ: Надо доказать, что BO = AO = OC

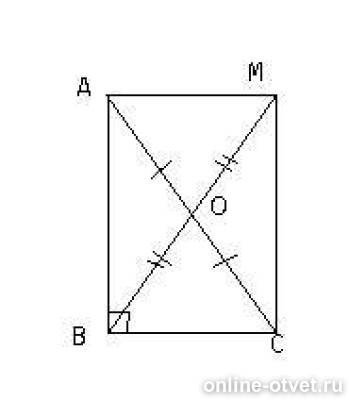
Рассмотрим прямоугольный треугольник ABC (угол B - прямой, BO - медиана). Продолжим BO, на линии отложим отрезок равный BO: OM (рисунок прилагается). Соединим точку M с точками A и C. Получится четырехугольник ABCM. Рассмотрим треугольники AOM и COB: 

AO = OC (О - середина AC)

BO = OM (по построению)

По 1 признаку равенства треугольников, ΔMOA = ΔBOC, следовательно все элементы в этих треугольниках равны:

АМ = BC; 

AC = BM - значит и их половины равны:

BO = AO = OC = OM

Что и требовалось доказать