Решение:
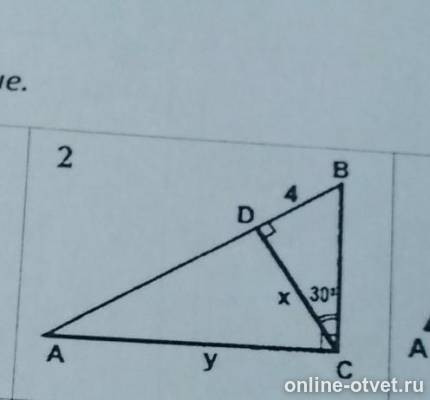
1) В Δ BCD ∠BDC = 90°, ∠DCB = 30°, тогда ∠DBC = 60°.
2) В Δ ABC  ∠BAC = 90° - ∠ABC = 90° - 60° = 30°.
3)  В Δ BCD ∠BDC = 90°, ∠DCB = 30°, тогда по теореме DB = BC, BC = 2·4 = 8.
4) В Δ ABC  ∠BAC = 30°., тогда BC = AB, AB = 2·8 = 16, AD = AB - BD = 16 - 4 = 12.
5) По теореме о пропорциональных отрезках в прямоугольном треугольнике CD² = DB·DA = 12·4 = 48
CD = √48 = √16·3 = 4·√3.
6) В Δ ACD ∠ADC = 90°, ∠DAC = 30°, тогда по теореме DC = AC, AC = 2·4√3 = 8√3.
(Можно было найти катет AC по-другому: по теореме Пифагора или 
по теореме о пропорциональных отрезках в прямоугольном треугольнике. CA² = AB·AD = 16·12 , CA = √16·4·3 = 4·2√3 = 8√3).
Ответ: х = CD = 4√3; у = AC = 8√3.