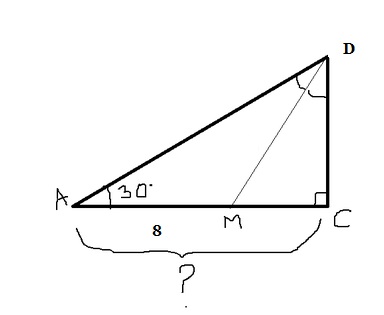
Вопрос по геометрии:
В треугольнике ACD известно, что ∠C = 90°, ∠A = 30°, отрезок DM — биссектриса треугольника. Найдите катет AC, если AM = 8 см.
- 11.04.2025 10:10
- Геометрия
- remove_red_eye 1022
- thumb_up 36
Ответы и объяснения 1
Ответ:
Дано:
∠C = 90°, ∠A = 30°,
AM = 8 см
отрезок DM — биссектриса треугольника
Найти: AC-?
Решение:
В прямоугольном треугольнике сумма его острых углов равна 900, тогда угол АВС = (90 – ВАС) = (90 – 30) = 600.
По условию, DМ биссектриса угла АВС, тогда угол СВМ = АВМ = АВС / 2 = 60 / 2 = 300.
Тогда треугольник АВМ равнобедренный, АМ = ВМ = 8 см, а угол АМВ = 180 – 30 – 30 = 1200.
По теореме косинусов, в треугольнике АВМ, определим длину стороны АВ.
AB^2 = AM^2 + BM^2 – 2 * AM * BM * cos120 = 64 + 64 – 2 * 8 * 8 * (-1/2) = 128 + 64 = 192
AB = 8 * √3 см
В прямоугольном треугольнике АВС,
cos BAC = AC / AB.
AC = AB * cos30 = 8 * √3 (√3/2) = 4 * 3 = 12 см
- 11.04.2025 12:31
- thumb_up 1
Знаете ответ? Поделитесь им!
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.