Вопрос по геометрии:
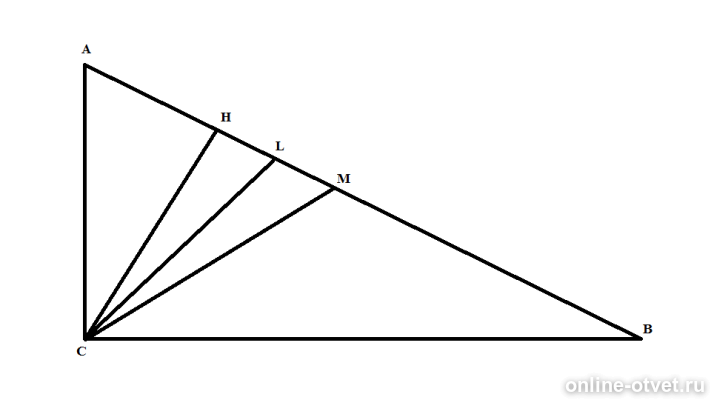
В прямоугольном треугольнике ABC угол C=90°.Катеты не равны.Отрезки CM,CL,CH являются соответственно медианой,биссектрисой и аысотой.Докажите что угол HCL= углу MCL
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок - бесплатно!
- 17.11.2017 00:21
- Геометрия
- remove_red_eye 13101
- thumb_up 20
Ответы и объяснения 1
1. угол АСL = углу LCB (т.к. CL - биссектриса)
2. СМ = 1/2 АВ (в соответствии с теоремой меридиана = 1/2 гипотенузы)
1/2 АВ = АМ=МВ (т.к. СМ - меридиана и делит гипотенузу пополам)
отсюда СМ = МВ
сответственно - СМВ это равнобедренный треугольник и у него углы у основания равны
поэтому угол МСВ = углу МВС
3. угол В (он же угол МВС=углу МСВ) можно выразить в треугольник АВС как 180 - (90- угол А) = 90 - угол А
в треугольнике АСН угол АСН можно выразить в треугольнике АСН как 180 - (90 - угол А) = 90 - угол А
следовательно угол АСН = углу МСВ
4. угол АСL (АСН + НСL) = углу LСВ (LСМ + МСВ)
при равенстве угол АСН = углу МСВ получается равенство, изначально стоящее в задаче в качестве доказывания HCL = LCM
- 18.11.2017 13:21
- thumb_up 9
Знаете ответ? Поделитесь им!
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.