Вопрос по геометрии:
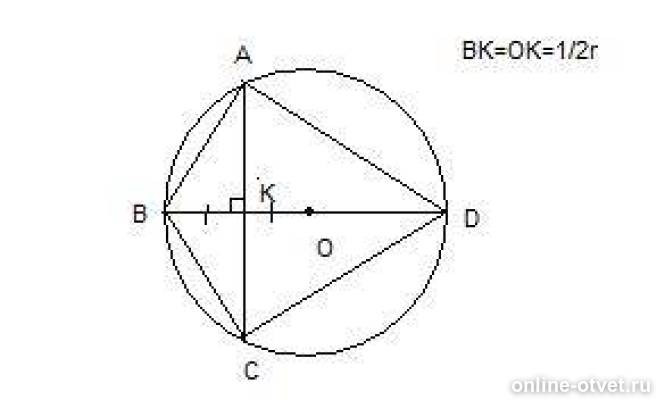
Отрезок BD- диаметр окружности с центром О.Хорда АС делит пополам радиус ОВ и перпендикулярна к нему .Найдите углы четырёхугольника ABCD и градусные меры дуг AB,BC,CD,AD.
- 24.09.2016 01:30
- Геометрия
- remove_red_eye 9901
- thumb_up 50
Ответы и объяснения 1
Т.к. вписанные углы BAD и BCD опираются на полуокружности, то они - прямые. Треугольники BAD и BCD - прямоугольные. Рассмотрим треуг-ик BAD. АК здесь - высота. Для катета АВ можно записать:
AB=√BK*BD=√1/2r*2r=√r²=r
BD=2r, значит АВ = 1/2 BD.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. Значит,
BC=√BK*BD=√1/2r*2r=√r²=r
Треугольники BAD и BCD, таким образом, равны по гипотенузе (она у них общая BD) и катетам АВ и ВС. Значит
АВ=ВС=30*2=60°
Вписанные равные углы ABD и CBD опираются на равные дуги AD и CD, углы равны половине этих дуг. Значит:
AD=CD=60*2=120°
- 25.09.2016 23:18
- thumb_up 1
Знаете ответ? Поделитесь им!
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.