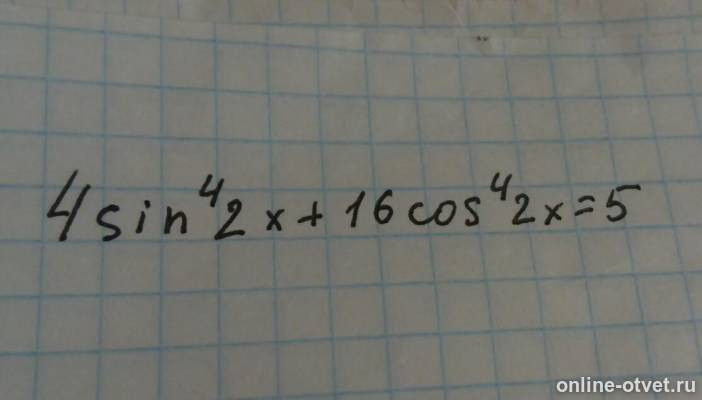Пожаловаться
- 05.02.2018 12:30
- Алгебра
- remove_red_eye 19949
- thumb_up 13
Ответы и объяснения 1
Разложим косинус 4х как косинус двойного угла 2х.
Применим формулу cos2a = 1- 2 sin^2 a .
4 sin^4(2x) +3( 1 - 2 sin^2(2x)) -1 =0;
4sin^4(2x)-6 sin^2(2x) +2=0;
2 sin^4(2x) - 3 sin^2(2x)+ 1 =0;
sin^2(2x)=t; 0≤t ≤1;
2 t^2 - 3t +1=0;
t1=1; ⇒ sin^2(2x)=1; ⇒ sin 2x = + -1;
⇒2x= pi/2 + pik;k∈Z. ⇒x=pi/4 + pik/2.
t2= 1/2;⇒ sin^2(2x)=1/2;⇒ sin(2x) = +-sgrt2/2;⇒
⇒2x= pi/4 +pi/2*k. ⇒x= pi/8 + pik/4.
Применим формулу cos2a = 1- 2 sin^2 a .
4 sin^4(2x) +3( 1 - 2 sin^2(2x)) -1 =0;
4sin^4(2x)-6 sin^2(2x) +2=0;
2 sin^4(2x) - 3 sin^2(2x)+ 1 =0;
sin^2(2x)=t; 0≤t ≤1;
2 t^2 - 3t +1=0;
t1=1; ⇒ sin^2(2x)=1; ⇒ sin 2x = + -1;
⇒2x= pi/2 + pik;k∈Z. ⇒x=pi/4 + pik/2.
t2= 1/2;⇒ sin^2(2x)=1/2;⇒ sin(2x) = +-sgrt2/2;⇒
⇒2x= pi/4 +pi/2*k. ⇒x= pi/8 + pik/4.
Пожаловаться
- 07.02.2018 00:17
- thumb_up 14
Знаете ответ? Поделитесь им!
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Новые вопросы
Интересные вопросы