Основанием 4-угольной пирамиды SABCD является прямоугольник ABCD со сторонами AB = 2 и AD = 3. Высота пирамиды длиной 12/√23 падает в точку пересечения диагоналей прямоугольника ABCD. Плоскость проходит через точку A, параллельна прямой BD, касается шара радиуса 1 с центром в точке S и пересекает ребро SC. В каком отношении она делит это ребро?

Question

knalincate · Answer

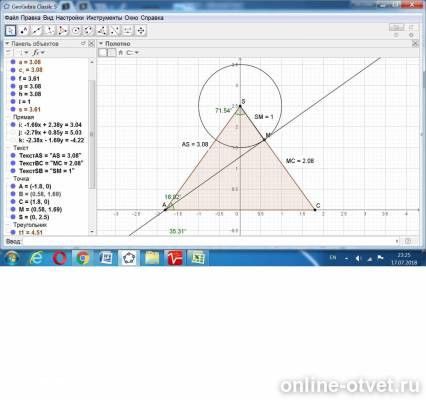
Проведём осевое сечение через боковые рёбра SA и SC.Половина диагонали АО = √(2² + 3²)/2 = √13/2.Угол А = arc tg(H/AO) = (12/√23)/(√13/2) = 24/√299 ≈ 1,387955837 .Этому тангенсу соответствует угол А = 0,946454578 радиан или 54,2278528°.Угол при вершине равен 180 - 2∠А = 71,5442944°.Найдём длину бокового ребра L.L = √(H² + (√13/2)²) = √((144/23)+(13/4)) = √(875/92) = 5√35/(2√23).Заданная плоскость рассечена секущей плоскостью по прямой АМ, где М - точка пересечения ребра SC.Опустим перпендикуляр из точки S на отрезок АМ в точку К.В прямоугольном треугольнике ASK определим угол ASK.∠ASK = arc sin(1/L) = arc sin(2√23)/(5√35) ≈ 71,07940953°.Как видим, угол между ребром SC и перпендикуляром к касательной к окружности R = 1 равен 0,464884873 градуса.Расстояние между точками К и М равно 0,00811395 .Поэтому с допустимой точностью можно принять, что окружность отсекает от ребра отрезок SM = 1.Ответ: ребро SC делится заданной секущей плоскостью в отношении 1 : 2,08..

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Есть сомнения?