РО=ТО=РТ - равносторонний, с углами по 60°, для определённости примем длину стороны этого треугольника за единицу
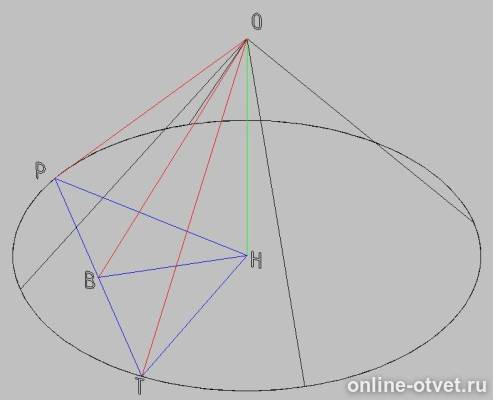
площадь сечения
S₁ = 1/2*1*1*sin(60°) = √3/4
Площадь боковой поверхности конуса
S₂ = π·r·l
где r - радиус основания, l - образующая, у нас l=1, радиус будем искать.
Площадь треугольника ОРТ через основание и высоту
S₁ = 1/2*РТ*ОВ = 1/2*1*ОВ = √3/4
ОВ = √3/2
Теперь с треугольником ОВН
ОН/ОВ = sin(60°)
ОН = OВ*sin(60°) = √3/2*√3/2 = 3/4
Теперь с треугольником ОТН
ТН² + ОН² = ОТ²
ТН² + (3/4)² = 1²
ТН² = 7/16
ТН = √7/4
---
S₂ = π·√7/4·1 = π√7/4
И требуемое отношение
S₁/S₂ = √3/4/(π√7/4) = √3/(π√7)