Вопрос по геометрии:
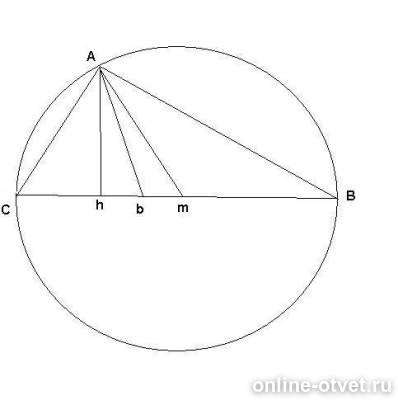
Доказать, что биссектриса прямого угла прямоугольного треугольника делит пополам угол между медианой и высотой, проведёнными к гипотенузе. подробно плизз))
- 15.08.2017 17:39
- Геометрия
- remove_red_eye 5940
- thumb_up 33
Ответы и объяснения 1
Треугольник АВС - прямоугольный, с НЕРАВНЫМИ катетами. Угол А = 90°. Аh - высота, Ab - биссектриса и Am - медиана из прямого угла. Угол hAC =90°-C = B ( так как треугольник hAС - прямоугольный). Угол bAC = 45°(так как Аb -бисск\ектриса). Тогда угол bAh = 45°-B.Угол bAB = 45°. Угол mAB = B (так как Аm - медиана из прямого угла, она равна Вm - это свойство и значит тр-к AmB - равнобедренный). Тогда угол bAm = угол bAB минус угол В = 45°-В.
Итак, углы bAh и bAm равны между собой, значит Ab - биссектриса угла hAm, что и требовалось доказать.
- 15.08.2017 22:55
- thumb_up 12
Знаете ответ? Поделитесь им!
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.