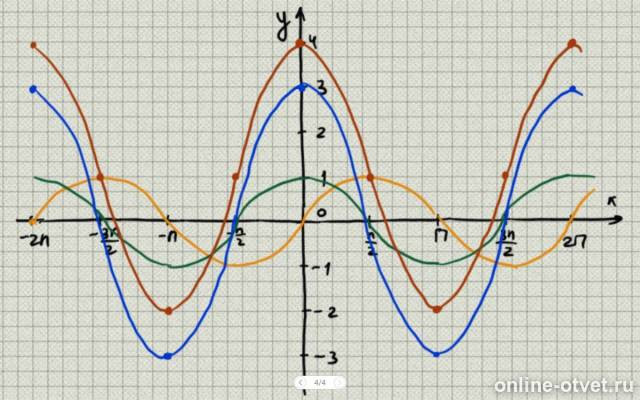
1. Сначала строим график y = sinx (оранжевый)

2. Затем с помощью параллельного переноса смещаем график на pi/2 влево по оси OX. Получаем y = sin(pi/2 + x) (зелёная)
*Также можно заметить, что sin(pi/2 + x) = cosx по формуле приведения. Тем самым на первом шаге сразу строить y = cosx (получится тоже зелёная)

3. Третьим шагом построим y = 3sin(pi/2 + x), для этого "растянем" зелёную функцию в 3 раза по оси OY (синяя функция).

4. К синей функции прибавляют 1. С помощью параллельного переноса y = 3sin(pi/2 + x) поднимаем на 1 вверх (ось OY). В итоге получаем красную функцию y = 3 sin(x + pi/2) + 1