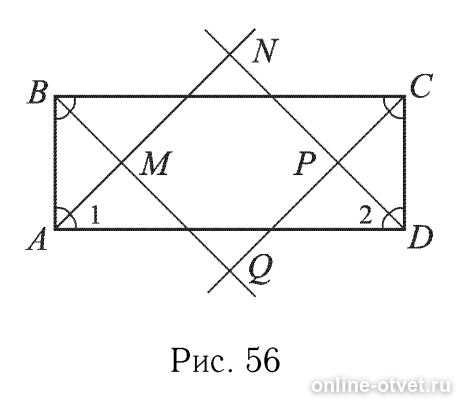
Решение. Пусть MNPQ — четырехугольник, образованный при пересечении биссектрис углов прямоугольника ABCD (рис. 56).
Четырехугольник MNPQ — прямоугольник.
Докажем, что MN=NP.
Треугольник AND - равнобедренный, так как угол 1 = углу 2= 45 градусов, поэтому AN=DN.
Ho AM=DP, так как треугольник ABM=тр.DPC (по стороне и прилежащим к ней углам). Таким образом, MN=AN-AM=DN-DP=NP.
Итак, в прямоугольнике MNPQ две смежные стороны равны, следовательно, MNPQ — квадрат.