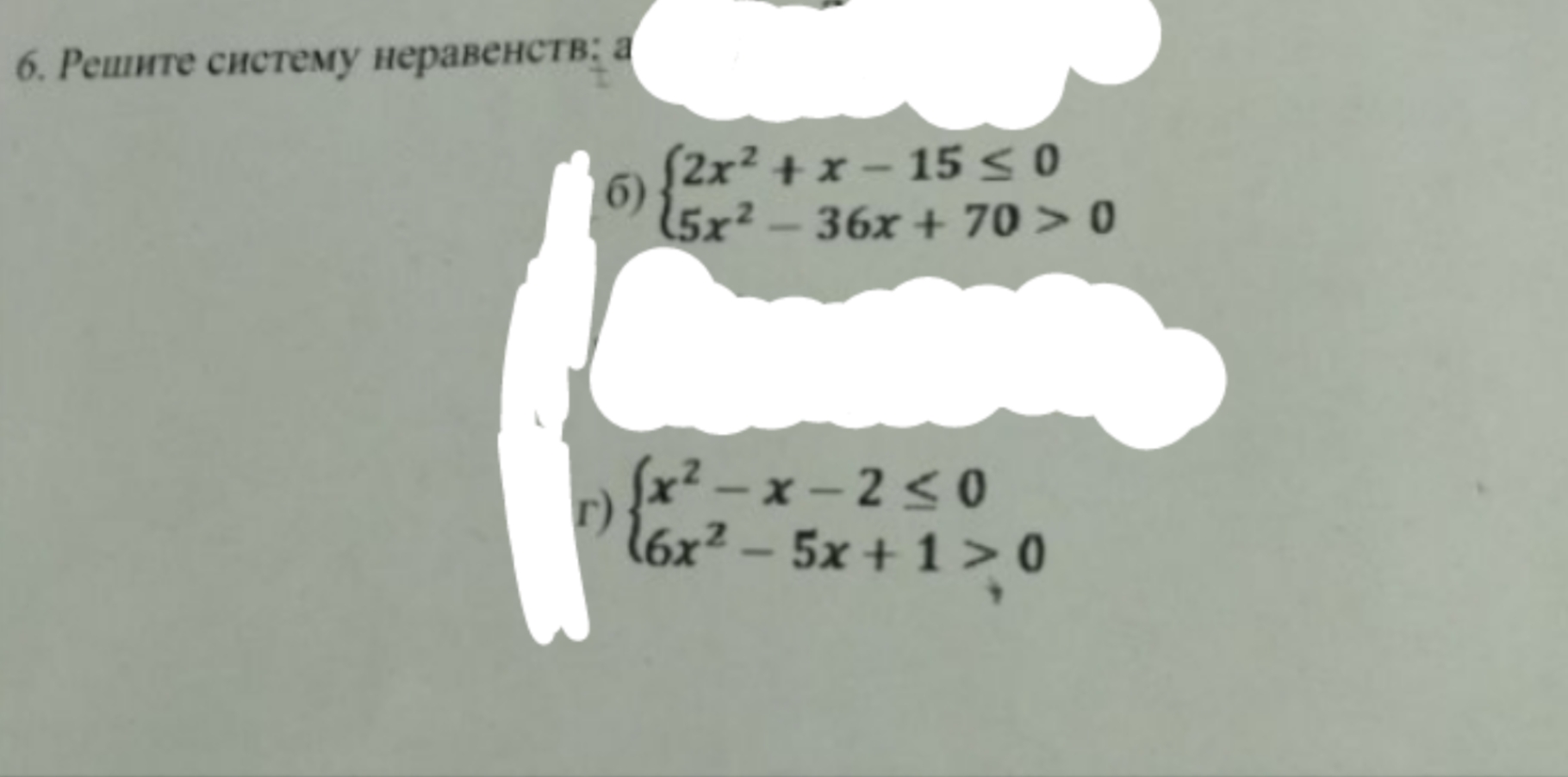Ответ:

б)

2x^2+x-15<=0

5x^2-36x+70>0

1)

2x^2+x-15=0

В квадратном уравнении ax2 + bx + c = 0

a = 2

b = 1

c = -15

x = -b ± D/2a,    D = b2 - 4ac

Найдем дискриминант квадратного уравнения:

D = b2 - 4ac = 12 - 4·2·(-15) = 1 + 120 = 121

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x1 = -b - √D/2·a = -1 - 121/2·2 = -1 - 11/4 = -12/4 = -3

x2 = -b + √D/2·a = -1 + 121/2·2 = -1 + 11/4 = 10/4 = 2.5

 

2)

5x^2-36x+70=0

В квадратном уравнении ax2 + bx + c = 0

a = 5

b = -36

c = 70

x = -b ± D2a,    D = b2 - 4ac

Найдем дискриминант квадратного уравнения:

D = b2 - 4ac = (-36)2 - 4·5·70 = 1296 - 1400 = -104

Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.

ответ:

-3<=x<=2.5

 

г)

x^2-x-2<=0

6x^-5x+1>0

 

x^2-x-2=0

В квадратном уравнении ax² + bx + c = 0

a = 1

b = -1

c = -2

x = -b ± D/2a,    D = b² - 4ac

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = (-1)² - 4·1·(-2) = 1 + 8 = 9

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x₁ = -b - √D/2·a = 1 - 9/2·1 = 1 - 3/2 = -2/2 = -1

x₂ = -b + √D/2·a = 1 + 9/2·1 = 1 + 3/2 = 4/2 = 2

(-1 ; 0]

 

6x^2-5x+1=0

В квадратном уравнении ax² + bx + c = 0

a = 6

b = -5

c = 1

x = -b ± D2a,    D = b² - 4ac

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = (-5)² - 4·6·1 = 25 - 24 = 1

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x₁ = -b - √D/2·a = 5 - 1/2·6 = 5 - 1/12 = 4/12 = 13 ≈ 0.33333

x₂ = -b + √D/2·a = 5 + 1/2·6 = 5 + 1/12 = 6/12 = 0.5

ответ:

(-1 ; +бесконечность)