Ответ:

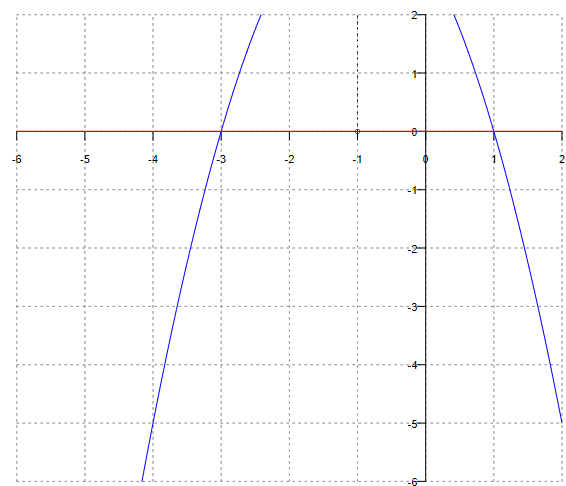
f(x)=-x2-2·x+3

1) Область определения функции. Точки разрыва функции.
2) Четность или нечетность функции.

f(-x)=-x2+2·x+3

Функция общего вида
3) Периодичность функции.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y

x=0,

y=3

Пересечение с осью 0X
y=0

-x2-2·x+3=0

Откуда:

x1=1,

x2=-3,

5) Исследование на экстремум.

y=-x2-2·x+3

1. Находим интервалы возрастания и убывания. Первая производная.

f′(x)=-2·x-2

Находим нули функции. Для этого приравниваем производную к нулю

-2·x-2=0

Откуда:

x=-1

 

(-∞;-1)

(-1;+∞)

f'(x) > 0 f'(x) < 0 функция возрастает функция убывает

В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

f″(x)=-2

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

-2=0

Для данного уравнения корней нет.
6) Асимптоты кривой.

y=-x2-2·x+3

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

limx→∞k·x+b-f(x)

Находим коэффициент k:


Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.

y=-x2-2·x+3

Найдем наклонную асимптоту при x → -∞:

limx→-∞k·x+b-f(x)

Находим коэффициент k:


Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.

 

2)

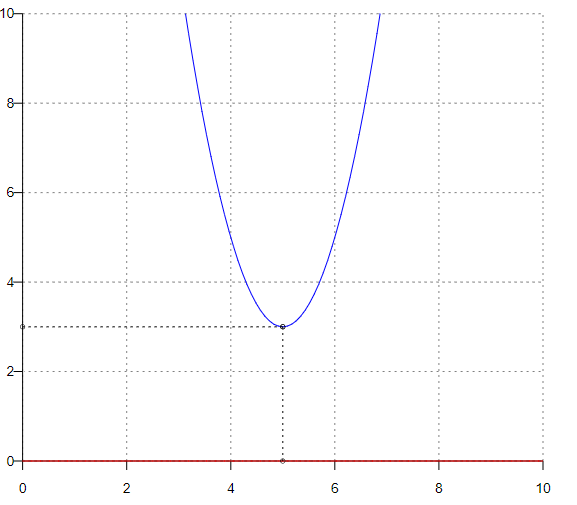
f(x)=2·x2-20·x+53

1) Область определения функции. Точки разрыва функции.
2) Четность или нечетность функции.

f(-x)=2·x2+20·x+53

Функция общего вида
3) Периодичность функции.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y

x=0

,

y=53

Пересечение с осью 0X
y=0

2·x2-20·x+53=0

Нет пересечений.
5) Исследование на экстремум.

y=2·x2-20·x+53

1. Находим интервалы возрастания и убывания. Первая производная.

f′(x)=4·x-20

Находим нули функции. Для этого приравниваем производную к нулю

4·x-20=0

Откуда:

x=5

 

(-∞;5)

(5;+∞)

f'(x) < 0 f'(x) > 0 функция убывает функция возрастает

В окрестности точки x = 5 производная функции меняет знак с (-) на (+). Следовательно, точка x = 5 - точка минимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

f″(x)=4

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

4=0

Для данного уравнения корней нет.
6) Асимптоты кривой.

y=2·x2-20·x+53

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

limx→∞k·x+b-f(x)

Находим коэффициент k:


Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.

y=2·x2-20·x+53

Найдем наклонную асимптоту при x → -∞:

limx→-∞k·x+b-f(x)

Находим коэффициент k:


Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.